La dysfonctiothèque et les sept ponts de Königsberg : Une leçon de mathématiques appliquée au management

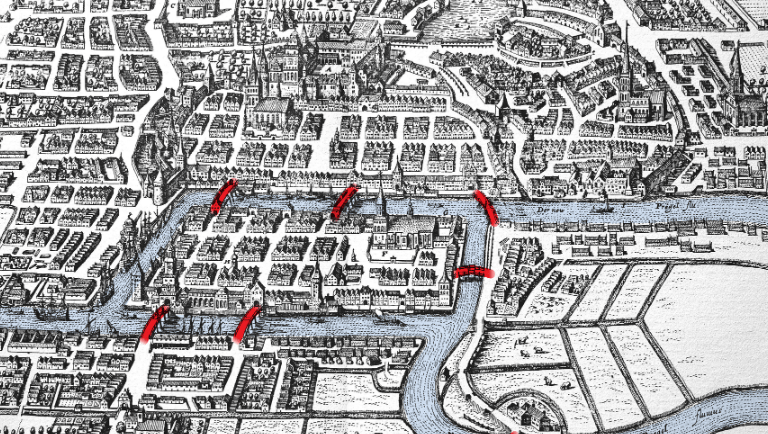
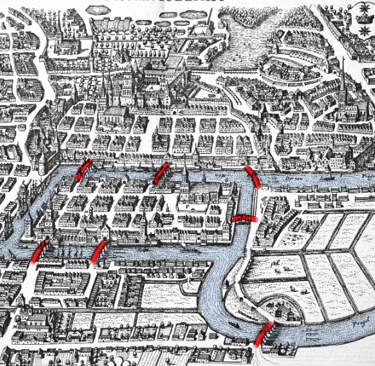
Au XVIIIe siècle, à Königsberg, capitale de la Prusse-Orientale, une énigme fascinait les habitants : était-il possible de parcourir chacun des sept ponts de la ville une seule fois sans repasser par le même ?

Cette question, en apparence simple, a donné naissance à la théorie des graphes, une branche fondamentale des mathématiques.

L'énigme des sept ponts de Königsberg

Le problème

La ville de Königsberg (avec ses ponts surlignés en rouge dans l’image ci-dessus par Amanda Montañez) fut le théâtre de cette célèbre énigme.

La réponse, comme l’ont découvert les habitants, est non : il est impossible de traverser tous les ponts en ne passant qu’une seule fois par chacun d’eux. La véritable question était donc de démontrer cette impossibilité.

La théière de Russell

Prouver une impossibilité est toujours un défi, comme l'illustre la célèbre théière de Russell :

« Si je suggérais qu'entre la Terre et Mars se trouve une théière de porcelaine en orbite elliptique autour du Soleil, personne ne serait capable de prouver le contraire, à condition que j’aie pris la précaution de préciser que la théière est trop petite pour être détectée par nos plus puissants télescopes. »

Si la réponse avait été "oui, il existe un chemin permettant de traverser tous les ponts sans en emprunter un deux fois", il aurait suffi de montrer ce chemin. Mais alors, comment prouver qu’il n’existe pas ?

La solution de Leonhard Euler

La solution à cette énigme a été apportée par le mathématicien Leonhard Euler. Il a modélisé les masses continentales de la ville sous forme de sommets (ou nœuds) et les ponts comme des arêtes.

Euler a démontré qu’un chemin traversant chaque arête une seule fois existe si et seulement si :
✅ Chaque sommet possède un nombre pair d’arêtes, ou
✅ Tous, sauf deux sommets, ont un nombre pair d’arêtes.

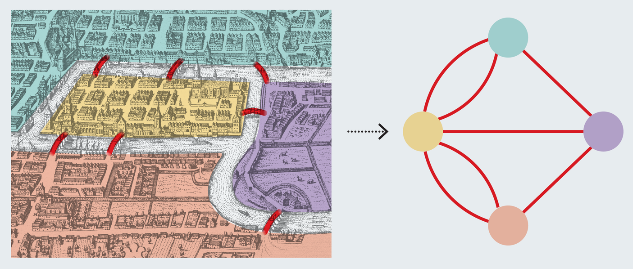
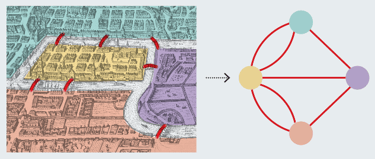
Visualisation du problème

Observons les deux cas suivants :

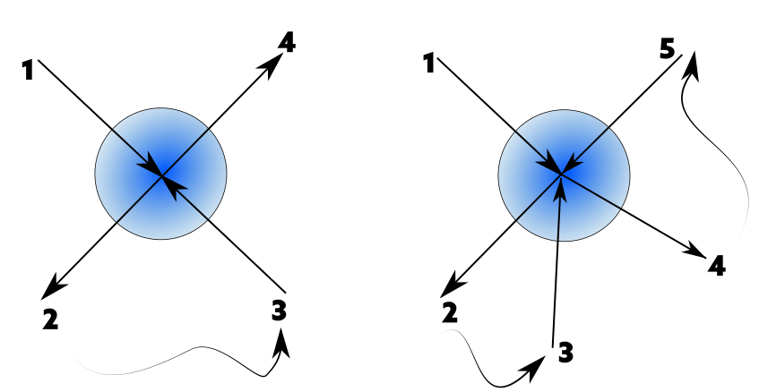
✅ Sommet avec un nombre pair d’arêtes :
Si une île possède quatre ponts, il est possible d’entrer par le pont 1, sortir par le pont 2, revenir par le pont 3 et repartir par le pont 4 sans se retrouver bloqué.

❌ Sommet avec un nombre impair d’arêtes :
Si une île possède cinq ponts, après avoir traversé tous les ponts, on se retrouve coincé, incapable de respecter la règle d’une seule traversée par pont.

Application chez Argios

Représentation des dysfonctionnements

Chez Argios, nous utilisons une approche similaire pour cartographier les dysfonctionnements au sein des équipes.

🔹 Chaque personne et chaque dysfonctionnement sont représentés comme des sommets uniques.
🔹 Lorsqu’un dysfonctionnement est identifié, une arête est créée entre la personne et ce dysfonctionnement.

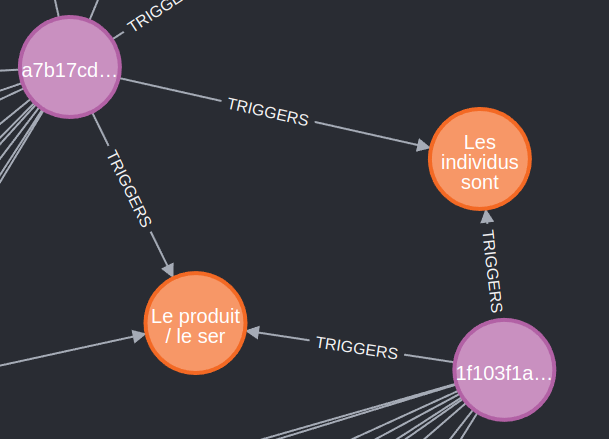
Cette méthode permet de visualiser les connexions entre différentes thématiques en mettant en évidence les dysfonctionnements communs.

Exemples de dysfonctionnements

Par exemple, le dysfonctionnement « Le produit/service ne possède pas toutes les compétences nécessaires à son bon fonctionnement » est souvent associé à « Les individus sont fatigués/résignés ».

Nous identifions également des nœuds denses, c’est-à-dire des dysfonctionnements rencontrés par plusieurs équipes indépendantes, comme « L'équipe gère trop de services ».

Analyse et recommandations

Si une équipe a identifié les dysfonctionnements X et Y, quelle est la probabilité qu’elle rencontre également le dysfonctionnement Z ?

À l’image des moteurs de recommandation, nous utilisons des graphes pour identifier les solutions les plus efficaces face à certains dysfonctionnements.

Conclusion

Bien que Königsberg ait été détruite pendant la Seconde Guerre mondiale, la théorie des graphes qu’elle a inspirée reste aujourd’hui un outil précieux.

Chez Argios, nous appliquons ces principes mathématiques pour optimiser la productivité, renforcer la compétitivité et accroître l’attractivité des entreprises. Rejoignez-nous et découvrez comment nous pouvons vous aider à atteindre vos objectifs.

En combinant IA générative et théorie des graphes, vous pouvez transformer votre entreprise et rester à la pointe de l’innovation. Contactez-nous pour en savoir plus sur nos solutions et services. Ensemble, atteignons de nouveaux sommets.